Мы уже размещали ранее статью В.И.Арнольда «О преподавании математики» (http://www.metodolog.ru/00640/00640.html ), повествующую о глубоком падении уровня преподавания во французских школах и вузах. Сегодня предлагаю читателю еще один труд на ту же тему. Снова математика и снова Франция. Статью размещаю не для того, чтобы позлорадствовать о том, как плохо «у них», а потому что не нашел хороших, талантливо выполненных материалов, рассказывающих о том, как сейчас «у нас».
Полагаю, что не лучше. Во всяком случае, мои наблюдения говорят именно об этом. Но не считаю себя достаточно подготовленным для формирования обобщений. А в прилагаемой работе – именно тот набор симптомов, который виден и в нашей действительности. Плюс – ужасно запущенная материальная база. Так что и этот колокол – про нас.
Редактор
http://www.school.edu.ru/news.asp?ob_no=29838
Уровень математической подготовки даже в развитых странах вызывает тревогу. Академик Владимир Игоревич Арнольд, например, считает, что школьное образование Франции, Англии и Америки просто гибнет в результате непродуманных реформ, проведенных там во второй половине XX века (см. "Наука и жизнь" № 12, 2000 г.). Умение пользоваться калькулятором привело к неумению мыслить аналитически и логически, понимать суть физических и математических задач (см. "Наука и жизнь" № 3, 2002 г.). О своем опыте преподавания в Парижском университете и размышлениях, связанных с ним, рассказывает доктор физико-математических наук Виктор Степанович Доценко.
Историки до сих пор спорят: как же могло получиться, что такие мудрые и образованные древние египтяне столь быстро разучились строить свои замечательные пирамиды? Все произошло на протяжении буквально нескольких поколений (на рубеже IV и V династий, около XXVI века до Р.Х.). И в самом деле, это была поразительная историческая катастрофа: веками учились, учились, по крохам совершенствовали мастерство, передавали все это из поколения в поколение, накапливали знания и опыт, потом выстроили свои три Великие пирамиды (Хеопса, Хефрена и Микерина) и вдруг разом все забыли, потеряли навык, умение и мастерство, перестали понимать элементарные вещи. Что особенно удивляет - это произошло как бы само по себе, безо всяких войн и нашествий варваров. Все, что было построено после, выглядело лишь как жалкое подобие Великих пирамид и сейчас представляет собой не более чем груду развалин.
Я теперь знаю, как такое может происходить: дело в том, что уже пятый год преподаю физику и математику в Парижском университете (Университет имени Пьера и Марии Кюри, известный также под именем "Paris VI", или "Jussieu"). Надо сказать, что Париж не последнее место на планете по уровню образования, а мой университет далеко не худший в Париже. Россия всегда несколько отстает от Запада, и, судя по тому, как энергично, а главное, во что нас реформирует родное Министерство образования, сейчас в Париже я могу наблюдать наше недалекое будущее. Сразу оговорюсь: я вовсе не претендую на роль "пророка из будущего" и поэтому буду стараться избегать обобщений. Мне все равно не по силам сравнивать средний уровень французского образования (о котором имею весьма смутное представление) со средним уровнем нынешнего российского образования (о котором тем более ничего не знаю). И если честно, вообще не понимаю, что такое "средний уровень образования". Я буду рассказывать только о своем личном опыте - так сказать, "что вижу, то и пою".
Сначала небольшая справка. Во Франции уже давно введен и действует "Единый государствен ный экзамен" (ЕГЭ), только называется он у них БАК (от слова "бакалавр"), но это сути не меняет. Мотивация введения французского БАКа была примерно та же, что и нашего ЕГЭ: чтобы поставить всех учеников в равные условия, чтобы свести на нет коррупцию на почве образования, чтобы унифицировать требования к выпускникам, ну и так далее. Короче, чтобы все было и по-честному, и по справедливости. Есть и отличие: у БАКа имеется несколько специализаций. Он может быть научным, когда приоритет (повышенный коэффициент) имеют экзамены по математике и физике; гуманитарным, когда приоритет отдается языкам, философии; экономическим и т. д. Человек, сдавший БАК, имеет право безо всяких вступительных экзаменов записаться в любой университет своего профиля (правда, только по месту жительства - прописка у французов очень даже имеется) и учиться в нем совершенно бесплатно (если не считать "комиссионного сбора" размером в три сотни евро в начале каждого учебного года). А если студент документально докажет, что доходы его семьи ниже определенного уровня, то может получать стипендию (совершенно независимо от своей успеваемости). Ученик, сдавший БАК с отметкой выше определенного уровня (больше чем 15 из 20), имеет право записаться на подготовительное отделение в одну из так называемых Гранд Эколь (самая известная из которых Эколь Нормаль Суперьер) - это что-то вроде элитных университетов, для поступления в которые после подготовительных курсов нужно выдержать еще и вступительные экзамены. Далее, в процессе учебы как в Гранд Эколь, так и в университете, в зимнюю и в весеннюю сессии происходит отсев. Если у студента сумма баллов всех экзаменов оказывается ниже определенного уровня, его выгоняют (или, в определенных ситуациях, оставляют на второй год). Отсев идет серьезный: в моем университете в первую зимнюю сессию выгоняют около 40 процентов студентов, в следующую - еще процентов 30 и т.д. В результате к концу второго года обучения остается едва ли четверть из тех, кто начинал учиться (фактически это растянутые на два года вступительные экзамены). Далее отсев тоже продолжается, хотя не столь интенсивно, и, наконец, венчают всю эту учебу два или три года так называемого ДEA, которое с некоторыми поправками соответствует нашей аспирантуре и которое, как и у нас, завершается (точнее, должно завершаться) диссертацией и ученой степенью. Естественно, что до этого уровня добираются только "самые-самые"... Ну и чтобы завершить это довольно скучное вступление, немного о себе: доктор физико-математических наук, профессор, занимаюсь теоретической физикой; в университете "Paris VI" преподаю математику и общую физику первокурсникам, а еще, в качестве "контрастного душа", читаю некий теоретический курс (уж не стану разъяснять о чем) и веду семинары для аспирантов последнего года Эколь Нормаль Суперьер (т. е. именно для тех, которые не только "самые-самые", но еще и "супер" и "экстра").
Ну вот, как видите, система образования задумана как будто совсем неплохо, все устроено вполне разумно, и даже деньги на все это есть (французы, правда, все время тоже говорят, что денег на образование катастрофически не хватает, но это просто оттого, что они не знают, что значит не хватает на самом деле). И тем не менее могу сообщить тем, кто еще не знает, что "хотели, как лучше, а получилось, как всегда" бывает не только в России. Французское образование (и я подозреваю, что далеко не только французское) - яркий тому пример.
В силу специфики своей деятельности в своем дальнейшем повествовании я буду иногда вынужден апеллировать к экспертам в области высшей математики. Я имею в виду тех, кто знает все четыре правила арифметики, а также умеет складывать дроби и в общих чертах знаком с таблицей умножения. Части текста, для понимания которых требуются столь специфические знания, я выделю курсивом.
Так вот, в этом учебном году я обнаружил, что среди пятидесяти моих учеников-первокурсников (у меня две группы) восемь человек считают, что три шестых (3/6) равно одной трети (1/3). Подчеркну: это молодые люди, которые только что сдали "научный БАК", то есть тот, в котором приоритет отдается математике и физике. Все эксперты, которым я это рассказывал и которые не имеют опыта преподавания в парижских университетах, сразу же становятся в тупик. Пытаясь понять, как такое может быть, они совершают стандартную ошибку, свойственную всем экспертам: пытаются найти в этом логику, ищут (ошибочное) математическое рассуждение, которое может привести к подобному результату. На самом деле все намного проще: им это сообщили в школе, а они, как прилежные ученики (а в университет попадают только прилежные ученики!), запомнили. Вот и все. Я их переучил: на очередном занятии (темой которого вообще-то было производная функции) сделал небольшое отступление и сообщил, что 3/6 равно 1/2, а вовсе не 1/3, как считают некоторые из присутствующих. Реакция была такая: "Да? Хорошо..." Если бы я им сообщил, что это равно 1/10, реакция была бы точно такой же.
В предыдущие два учебных года процентов десять-пятнадцать моих студентов систематически обнаруживали другое, не менее "нестандартное" математическое знание: они полагали, что любое число в степени -1 равно нулю. Причем это была не случайная фантазия, а хорошо усвоенное знание, потому что проявлялось неоднократно (даже после моих возражений) и срабатывало в обе стороны: если обнаруживалось что-либо в степени -1, то оно тут же занулялосъ, и наоборот, если что-либо требовалось занулить, подгонялась степень -1. Резюме то же самое: их так научили.
Вот чему несчастных французских детей никак не могут по-настоящему научить, так это обращаться с дробями. Вообще, дроби (их сложение, умножение, а особенно деление) - постоянная головная боль моих студентов. Из своего пятилетнего опыта преподавания могу сообщить, что сколько-нибудь уверенно обращаться с дробями могли не больше десятой части моих первокурс ников. Надо сказать, что арифметическая операция деления - это, пожалуй, самая трудная тема современного французского среднего образования. Подумайте сами, как объяснить ребенку, что такое деление: небось станете распределять поровну шесть яблочек среди троих мальчиков? Как бы не так. Чтобы рассказать, как учат делению во французской школе, я опять вынужден обращаться к экспертам. Пусть не все, но кое-кто из вас еще помнит правило деления в столбик. Так вот, во французской школе операция деления вводится в виде формального алгоритма деления в столбик, который позволяет из двух чисел (делимого и делителя) путем строго определенных математических манипуляций получить третье число (результат деления). Разумеется, усвоить этот ужас можно, только проделав массу упражнений, и состоят эти упражнения вот в чем: несчастным ученикам предъявляются шарады в виде уже выполненного деления в столбик, в котором некоторые цифры опущены, и эти отсутствующие цифры требуется найти. Естественно, после всего этого, что бы тебе ни сказали про 3/6, согласишься на что угодно.
Разумеется, кроме описанных выше, так сказать, "систематических нестандартных знаний" (которым научили в школе) имеется много просто личных, случайных фантазий. Некоторые из них очень смешные. Например, один юноша как-то предложил переносить число из знаменателя в числитель с переменой знака. Другая студентка, когда косинус угла между двумя векторами у нее получился равным 8, заключила, что сам угол равен 360 градусов умножить на восемь, ну и так далее. У меня есть целая коллекция подобных казусов, но не о них сейчас речь. В конце концов, то, что молодые люди еще способны фантазировать, - это не так уж плохо. Думать в школе их уже отучили (а тех, кого еще не отучили, в университете отучат - это уж точно), так пусть пока хоть так проявляют живость ума (пока они, живость и ум, еще есть).
Довольно долго я никак не мог понять, как с подобным уровнем знаний все эти молодые люди сумели сдать БАК, задачи в котором, как правило, составлены на вполне приличном уровне и решить которые (как мне казалось) можно, лишь обладая вполне приличными знаниями. Теперь я знаю ответ на этот вопрос. Дело в том, что практически все задачи, предлагаемые на БАКе, можно решить с помощью хорошего калькулятора - они сейчас очень умные, эти современные калькуляторы: и любое алгебраическое преобразование сделают, и производную функции найдут, и график ее нарисуют. При этом пользоваться калькулятором при сдаче БАКа официально разрешено. А уж что-что, а быстро и в правильном порядке нажимать на кнопочки современные молодые люди учатся очень лихо. Одна беда - нет-нет да и ошибешься, в спешке не ту кнопочку нажмешь, и тогда получается конфуз. Впрочем, "конфуз" - это с моей, старомодной, точки зрения, а по их, современному, мнению - просто ошибка, ну что поделаешь, бывает. К примеру, один мой студент что-то там не так нажал, и у него получился радиус планеты Земля равным 10 миллиметрам. А, к несчастью, в школе его не научили (или он просто не запомнил), какого размера наша планета, поэтому полученные им 10 миллиметров его совершенно не смутили. И лишь когда я сказал, что его ответ неправильный, он стал искать ошибку. Точнее, он просто начал снова нажимать на кнопочки, но только теперь делал это более тщательно и в результате со второй попытки получил правильный ответ. Это был старательный студент, но ему было абсолютно "до лампочки", какой там радиус у Земли: 10 миллиметров или 6400 километров, - сколько скажут, столько и будет. Только не подумайте, что проблему можно решить, запретив калькуляторы: в этом случае БАК просто никто не сдаст, дети после школы вынуждены будут вместо учебы в университетах искать работу, и одновременно без работы останется целая армия университетских профессоров - в общем, получится страшный социальный взрыв. Так что калькуляторы трогать не стоит, тем более, что в большинстве случаев ученики правильно нажимают на кнопочки.
Теперь о том, как, собственно, учат математике и физике в университете. Что касается математики, то под этой вывеской в осеннем семестре изучаются три темы: тригонометрия (синусы, косинусы и т. д.), производные функций и несколько интегралов от стандартных функций - в общем, все то, что и так нужно было знать, чтобы сдать БАК. Но в университете, как это часто бывает, учат все сначала, чтобы научить наконец "по-настоящему".
Что касается тригонометрии, то ее изучение сводится к заучиванию таблицы значений синуса, косинуса и тангенса для стандартных углов 0, 30, 45, 60 и 90 градусов, а также нескольких стандартных соотношений между этими функциями. Старательные студенты, которых в действительности не так уж мало, все это знают и так. Однако вот ведь какая закавыка, я каждый год упорно задаю своим ученикам один и тот же вопрос: кто может объяснить, почему синус 30 градусов равен 1/2? Я преподаю уже пять лет, и каждый год у меня около пятидесяти учеников; так вот, из двухсот пятидесяти моих учеников за все время на этот вопрос мне не ответил ни один человек. Более того, по их мнению, сам вопрос лишен смысла: то, чему равны все эти синусы и косинусы (так же, впрочем, как и все остальные знания, которыми их пичкали в школе, а теперь продолжают пичкать в университете), - это просто некая данность, которую нужно запомнить. И вот каждый год я как последний зануда пытаюсь их в этом разубеждать, пытаюсь рассказывать, что откуда берется, какое отношение все это имеет к миру, в котором мы живем, тужусь изо всех сил рассказывать так, чтобы было интересно, а они смотрят на меня, как на придурка, и терпеливо ждут, когда же я наконец угомонюсь и сообщу им, что, собственно, нужно заучить на память. Своим большим успехом я считаю, если к концу семестра один или два человека из группы раз-другой зададут мне вопрос "почему?". Но достичь этого мне удается не каждый год...
Теперь производная функции. Милые эксперты, не пугайтесь: никакой теоремы Коши, никакого "пусть задано эпсилон больше нуля..." тут не будет. Когда я только начинал работать в университете, некоторое время ходил на занятия моих коллег - других преподавателей, чтобы понять что к чему. И таким образом я обнаружил, что на самом деле все намного-намного проще, чем нас когда-то учили. Спешу поделиться своим открытием: производная функции - это штрих, который ставится справа вверху от обозначения функции. Ей-богу, я не шучу - прямо так вот и учат. Нет, разумеется, это далеко не все: требуется заучить свод правил, что произойдет, если штрих поставить у произведения функций и т.п.; выучить табличку, в которой изображено, что этот самый штрих производит со стандартными элементарными функциями, а также запомнить, что если результат этих магических операций оказался положительным, значит, функция растет, а если отрицательным - убывает. Только и делов. С интегрированием точно такая же история: интеграл - это такая вот вертикальная карлючка, которая ставится перед функцией, затем даются правила обращения с этой самой карлючкой и отдельное сообщение: результат интегрирования - это площадь под кривой (и на кой им нужна эта площадь?..).
С преподаванием физики дела обстоят похоже, только рассказывать про это скучно - здесь не так много смешного. Потому очень кратко (просто для полноты картины): курс физики в первом семестре в Университете имени Пьера и Марии Кюри начинается почему-то с линейной оптики (при этом параллельно на лабораторных занятиях студенты зачем-то изучают осциллограф), затем - два занятия подряд они зубрят наизусть огромную таблицу с размерностями физических величин (то есть как выражается в килограммах, секундах и метрах, скажем, гравитационная постоянная и т. п.; замечу попутно - при этом они понятия не имеют, что такое гравитационная постоянная), затем - механика (столкновения шариков, равновесие сил и т. п.), и наконец венчает осенний семестр почему-то гидродинамика. Почему именно такая выборка - понятия не имею, возможно, это то немногое, что знает главный координатор (и лектор) нашей секции. Почему именно в таком порядке? Да, собственно, какая разница, в каком порядке все это зубрить...
Бедные Мария и Пьер Кюри... Они на том свете небось места себе не находят от стыда.
Попробую предложить отдаленную аналогию всей этой ахинеи для гуманитариев. Представьте себе, что программа университетского курса под названием "Русская литература" состоит из следующих разделов: 1. Творчество А. П. Чехова; 2. Лингвистический анализ произведений русских и советских писателей XIX и XX веков; 3. "Слово о полку Игореве"; 4. Творчество А. Платонова. И на этом все...
Что же касается аспирантов Эколь Нормаль Суперьер (то есть тех, которые "супер-самые-самые"), то здесь ситуация совершенно иная. Эти ребята прошли такой суровый отбор, что ни вольных фантазеров, ни тем более разгильдяев здесь уже не встретишь. Более того, и с дробями у них все в порядке, и алгебру они знают прекрасно, и еще много-много всего, что им полагается знать к этому возрасту. Они очень целеустремленные, работоспособные и исполнительные, и с диссертациями у них, я уверен, будет все в полном порядке. Одна беда - думать они не умеют совершенно. Исполнить указанные, четко сформулированные преподавателем манипуляции - пожалуйста, что-нибудь выучить, запомнить - сколько угодно. А вот думать - никак. Эта функция организма у них, увы, атрофирована полностью. Ну а кроме того, теоретическую физику они, конечно, не знают совершенно. То есть они, конечно, знают массу всевозможных вещей, но это какая-то пестрая, совершенно хаотичная мозаика из массы всевозможных маленьких "знаний", которые они с успехом могут использовать, только если вопросы им приготовлены в соответствии с заранее оговоренными правилами, совместимыми с этой мозаикой. Например, если такому аспиранту задается некий вопрос, то ответом на него должно быть либо "знание А", либо "знание В", либо "знание С", потому что если это ни А, ни В, ни С, он станет в ступор, который называется "так не бывает". Хотя, конечно, и у аспирантов Эколь Нормаль Суперьер бывают довольно смешные дыры в знаниях - но тут несчастные детишки совершенно не виноваты - это преподаватели у них были такие. Например, из года в год я обнаруживаю, что никто из моих слушателей (аспирантов последнего года Эколь Нормаль Суперьер!) не способен взять Гауссов интеграл и вообще не имеет представления о том, что это такое. Ну это как если бы человек писал диссертацию, скажем, о месте природы в поэзии позднего Пушкина и при этом не имел представления о том, что такое синонимы. Но, вообще, конечно, из этих аспирантов получатся прекрасные исполнители, как те "роботы-исполнители" из давнего фильма "Москва - Кассиопея"... И поэтому мне больше нравится преподавать первокурсникам университета: там все-таки еще есть хоть небольшая надежда кого-то чему-то научить...
Мне их так жалко, этих детишек! Вы только представьте: из года в год с раннего детства зубрить, зубрить и зубрить весь этот бред... Но ведь понятно, что вызубрить все невозможно. Даже у самых прилежных учеников хоть в чем-то, но будут пробелы. На практике это иногда выглядит дико (по крайней мере для меня). Представьте себе: прилежный студент, умеет находить производные, умеет интегрировать (то есть он вызубрил все правила, про "штрих" и "вертикальную карлючку"), но вот дроби складывать не умеет. Или, допустим, складывать умеет, а вычитать - никак - ну не выучил вовремя! При этом он может знать всю таблицу умножения, но вот чему равно 6 умножить на 7 - нет (может, он просто проболел в тот день, когда учитель в школе это сообщал). Теперь вы, надеюсь, поняли, что на самом деле 3/6 может равняться не только 1/3, а вообще чему угодно. Если хотите, это можно назвать "пятым правилом арифметики": сколько скажем, столько и будет!
Мне неизвестно, сколько времени здесь продолжается весь этот образовательный "апокалипсис", может, лет десять, может, чуть меньше, но то, что в школы уже пришли преподаватели "нового поколения" - выпускники таких вот университетов - это точно, я вижу по своим ученикам. Что же касается моих коллег - нынешней университетской профессуры... Нет, с арифметикой у них все в порядке, и, вообще, в каком-то смысле все они довольно грамотные люди - стареющее вымирающее поколение. Но, с другой стороны, когда происходит такой всеобщий бардак в образовании, вольно или невольно, но тупеют все - не только ученики, но и преподаватели, видимо, это какой-то неизбежный закон природы. Разврат развращает...
В этом учебном году на семестровой контрольной одной из задач была такая (я думаю, наши восьми-, а может, и семиклассники ее бы оценили): "Воздушный шар летит в одном направлении со скоростью 20 км/час в течение 1 часа и 45 минут. Затем направление движения меняется на заданный угол (60°), и воздушный шар летит еще 1 час и 45 минут с той же скоростью. Найти расстояние от точки старта до точки приземления". Перед контрольной на протяжении двух недель среди преподавателей университета шла бурная дискуссия - не слишком ли сложна эта задача для наших студентов. В конце концов решили рискнуть выставить ее на контрольную, но с условием, что те, кто ее решит, получат дополнительно несколько премиальных очков. Затем в помощь преподавателям, которые будут проверять студенческие работы, автор этой задачи дал ее решение. Решение занимало половину страницы и было неправильным. Когда я это заметил и поднял было визг, коллеги тут же успокоили меня очень простым аргументом: "Чего ты нервничаешь? Все равно эту задачу никто не решит..." И они оказались правы. Из полутора сотен студентов, писавших контрольную, ее решили только два человека (и это были китайцы). Из моих пятидесяти учеников примерно половина даже не попыталась ее решать, а у тех, кто сделал такую попытку, спектр полученных ответов простирался от 104 метров до 108 500 километров. Отдавая работу той студентке, которая умудрилась получить расстояние в 108,5 тысячи километров, я попытался было воззвать к ее здравому смыслу: дескать, ведь это два с половиной раза облететь вокруг земного шара! Но она мне с достоинством ответила: "Да, я уже знаю - это неправильное решение". Такие вот дела...
Читатель небось уже измучился в ожидании ответа на давно созревший вопрос: "Как же такое может быть?!" Ведь Франция - высокоразвитая культурная страна, в которой полным-полно умных образованных людей. Это один из главных мировых лидеров и в теоретической физике, и в математике, и в высоких технологиях, страна, где по российским понятиям "все хорошо". И в конце концов куда подевалась выдающаяся французская математическая школа "Бурбаки"? И вообще, при чем тут "Единый государственный экзамен"?
Про "Бурбаки" ответить проще всего. Эта школа никуда не делась, она продолжает функционировать, но при этом стала похожей на "черную дыру": людей (и талантливых людей!) она продолжает в себя "всасывать", но что там у нее делается внутри, те, кто находится снаружи, уже не знают. Это стало чем-то вроде "игры в бисер" Германа Гессе. Хотя мощная математическая традиция "Бурбаки" во французском обществе конечно же осталась. Именно поэтому несчастных детишек здесь так мучают шарадами про деление в столбик. Или, к примеру, когда нужно было решить уравнение 5х + 3 = 0, один мой студент исписал целую страницу рассуждениями про структуру и счетность множества решений такого типа уравнений, но само уравнение решить так и не смог. Хорошо известно, что получается, если из учения, веры или науки уходит дух, а остается один формальный ритуал: маразм.
Что же касается "как же такое может быть?!", то, как видите, может, очень даже может! Правда, я подозреваю, только до поры до времени. Во-первых, нужно иметь в виду, что вся эта катастрофа в образовании началась не так уж давно, и когда говорят про умных и образованных людей, то это в действительности очень тонкий слой общества (на котором на самом деле все и держится), состоящий из пожилых, стареющих (и вымирающих) "динозавров". И подпитки в этот слой сейчас просто не происходит (точнее, она происходит за счет китайцев и прочих там русских). Во-вторых, существует и совершенно другая точка зрения на происходящее. Этот крайне циничный взгляд на современное общество как-то растолковал мне один мой коллега по университету (огромный патриот Франции, по происхождению поляк, несколько лет проучившийся в Москве, прекрасно говорящий по-русски, большой знаток русской литературы). Он очень умный человек, тоже преподает и прекрасно видит, что происходит, но при этом считает, что никакой катастрофы нет, а наоборот, все правильно, все развивается как надо. Дело в том, что современному развитому обществу нужны только хорошие исполнители. Творческие, думающие люди, конечно, тоже требуются, но буквально единицы. Поэтому вся система образования должна быть настроена на отбор, выращивание и дрессировку именно хороших исполнителей, а учить думать молодых людей совершенно не нужно: в современном обществе это только повредит их будущей профессиональной деятельности, какой бы она ни была. Что же касается творческих личностей, то о них особенно беспокоиться не следует: тот, кто действительно талантлив, так или иначе все равно пробьется. В этом смысле, по большому счету, совершенно не важно, каким предметам мы их тут, в университете, учим (по крайней мере на первых курсах). Вместо физики с математикой вполне можно было бы заставлять зубрить, например, латынь (вот только специалистов таких сейчас не сыщешь). Все равно в будущей профессиональной деятельности никакое понимание физики с математикой им не понадобится. На уровне школы и университета важно просто производить отбор и дрессировку самых послушных, трудолюбивых и исполнительных, вот и все. А для тех, кто вылетает из этой системы, для тех, кто идет в "отходы", существуют метлы для подметания улиц, кассовые аппараты в супермаркетах, заводские конвейеры и т. д. Вы вон в Советском Союзе в свое время напроизводили миллионы образованных "думающих" инженеров - и что? По части своих прямых профессиональных обязанностей они, как правило, ни черта делать не умели, а предпочитали размышлять о судьбах мира, о смысле жизни, о Достоевском... Причем, согласитесь, сами эти, так сказать, "думающие образованные инженеры" сплошь и рядом чувствовали себя несчастными людьми: невоплощенные мечты о великих свершениях, нереализованные таланты, мировая скорбь и тому подобное. А тут жизненные претензии и запросы, как личные, так и профессиональные, четко алгоритмированы, и все счастливы и довольны...
Я думаю, мысль понятна, и дальше можно не распространяться. Обо всем этом уже писано-переписано в бесчисленных утопиях и антиутопиях. Мне лично подобная точка зрения на развитое современное общество крайне несимпатична, но это отнюдь не значит, что она ошибочна. Мне кажется, что в подобной системе никакие таланты никуда не пробьются (просто потому, что их некому будет учить), и тогда люди, точнее, "роботы-исполнители" очень быстро разучатся строить "Великие пирамиды". Но, может, я и ошибаюсь...
Теперь, надеюсь, понятно, при чем тут "Единый государственный экзамен"? Когда люди, вместо того чтобы думать самим и учить думать своих детей, пытаются в конечном итоге все на свете сводить к алгоритмам и тупым тестам, наступает всеобщее отупение. Впрочем, что тут первично, а что вторично, не знаю: вполне возможно, что все эти БАКи, ЕГЭ и прочие тесты не более чем следствие (а вовсе не причина) всеобщего, скажем так, "радикального упрощения мышления" в развитом обществе. В моей молодости экзамены в стиле ЕГЭ проводились только на военной кафедре, что как раз было вполне оправданно и понятно: "приказ начальника - закон для подчиненного", и все тут, а думать при этом было противопоказано. Теперь подобный стиль обучения похоже становится всеобщим. По мне так уж лучше пусть будет коррупция, чем кристально честное общество исполнительных роботов-идиотов. Хотя, впрочем, у меня есть сильные подозрения, что в этом смысле России ничего особенно серьезного не грозит. У нас сплошь и рядом вязнут и дохнут не только благие начинания, но, к счастью, и идиотские.
Ну а если подобная "алгоритмизация" жизни и в самом деле есть магистральная дорога дальнейшего развития человечества (в конце концов, если это эффективно, то почему нет?), что ж, тогда мне просто останется пожелать ему счастливого пути. Удачи вам, ребята, дальше продолжайте без меня, я остаюсь...
Доктор физико-математических наук В. ДОЦЕНКО.
Комментарии
Re: Пятое правило арифметики
Как думаете, долго ли ещё сможет оставаться таким положение вещей в образовании? Когда-то ведь и жареный петух должен проснуться, чтобы клюнуть больно. Конечно, умных людей никогда не будет много. Кто-то ведь должен быть исполнителем чужих идей и будующие исполнители прекрасно понимают свою будующую роль и не стремятся что-то изменять, но ведь откуда-то должны браться, просачиваться на свет и генераторы идей. Откуда же они беруться, как крупицы золота в породе? Мне кажется, они формируются из тех, кто получил образование, получил диплом об образовании, но понимая, что на самом деле ничего не знает, начинает докапываться до всего уже сам, особенно если этого требует его профессия и то место работы, куда он устроился. Когда полученные знания становятся нужны на практике, то после пары лет своего личного дообразования уже самостоятельно по книгам и с помощью колег по работе, человек превращается из молодого специалиста в СПЕЦИАЛИСТА. Это при большом личном желании и упорстве.
Re: Пятое правило арифметики
Петух проснулся и уже давно клюет. Так же как и идет разделение на морлоков и элоев.
В нашем образовании катастрофа многопланова - на мой взгляд, конечно. И вслед за петухом угадывается другой зверек - внешне мягкий и пушистый.
Re: Пятое правило арифметики
Во времена работы над ЖСТЛ Генриху Сауловичу Альтшуллеру мы высылали работы разного уровня по жизни и деятельности творческих личностей. Одна из работ которую я выслал касалась Жан-Анри Фабра (1823-1915г) французского энтомолога, писателя, преподавателя.
К сожаления, как обычно, я опоздал и работа по ЖСТЛ, наверное в черне уже была завершена. Ничего из моих материалов в ЖСТЛ не вошло.
Получил лишь отзыв "Интересный дядечка!" Г.С. Альтшуллер
А жаль, о нем у нас большинство ничего не знает.
В лице Фабра мы имеем пример человека совершенно изумительной и разносторонней одаренности, соединенной с исключительным трудолюбием. Это фигура подобная Леонардо да Винчи, Ломоносову, Копернику. (А.А. Любищев)
Известный исследователь и знаток мира насекомых, их поведения, инстинктов. Блестящий французский прозаик, поэт. Мировой чемпион самоучек. Самый выдающийся из людей которые сами себя создали. Им написано множество увлекательных книг по разным отраслям знаний.
1862-65гг "Основы науки", "Агрономическая химия", "Физика", "Книга о земле", "Небо", "История полена", "Книга об истории", "Научные беседы дяди Поля с его племянником".
1870г "Органическая химия", "Новая арифметика", расcчитанная на все учреждения народного образования с приложением 1880 задач и упражнений". Позже вышли такие же пособия по геометрии, алгебре, тригонометрии. "Курс элементарной физики", "Вредители", "Рассказы дяди Поля о насекомых вредящих в сельском хозяйстве", "Элементарная астрономия", "Научное чтение по зоологии", "Наши слуги. Рассказы дяди Поля о животных полезных для с/х.", "Научные чтения по ботанике", "Промышленность. Простые рассказы дяди Поля о происхождении, истории, способе изготовления наиболее распространенных предметов обихода", "Домоводство", "Курс космографии с литературным чтением", "Книга полей", "Сельскохозяйственная арифметика", "Теоретическая и практическая, для начальных школ с приложением 600 задач и упражнений относящихся к агрономии", "Курс механики", "Маленькие девочки", "Химия дяди Поля", "Изобретатели и их изобретения", "Почвы и минералы, основы естественной истории"...
Его "Энтомологические воспоминания" это эпоха в развитии науки и литературы о науке. Отрывки из сочинений Фабра при жизни печатались на обложках тетрадей.
111 пожизненно изданных пособий, книг.
Энтомологические воспоминания. 1-й том итог 25 летних наблюдений. 30 лет выходили в свет тома "Воспоминаний". 1907г 84г 10й том "Сувенир энтомоложник" 220 повестей о мире насекомых".
Суть его книг: "Учение не имеет право быть горьким. Оно должно быть интересным. Дело, суть которого не понятна, вызывает омерзение".
Так вот, касательно образования во Франции, была эта деятельность Фабра и было другое.
Школа во Франции - смесь казармы и монастыря. Централизация учебной части доведена до крайности. В один и тот же час во всех школах выполняется одна и та же работа. Четыре раза в день богослужение. Так готовили будущих учителей. Отсекалось все что пахнет материализмом: физика, растения, насекомые, минералы.
Вывод: борьба стандарта и творчества была, есть и будет. И все с благими намерениями. И нет здесь выбора между сражающими сторонами, а только их единство. И то, и другое.
Re: Пятое правило арифметики
Вы описали образование Франции каких времен? До революционного преобразований? В принципе в Европе есть два континентальных (германское и французское) и англосаксонское образование. Отечественное идет от германского, американское, например, от англосаксонского. Перекос в практику (в том числе в "алгоритмичность"!) всегда была специфика англосаксонского, а вот жесткостью (палочностью) особенно среднего образования отличались абсолютно все
Таким образом, речь не обязательно идет между "стандартом" и творчеством. Почитайте о всех сложностях (полувековые судя по обсуждениям в Сенате и постановлениям их президента) среднего американского образования. А они сделали выбор как раз на свободное проявление творчества учащегося - в ущерб систематичности. О приоритете творчества можно прочитать в переведенной книге Карло Роджерса и Фрейберга "Свобода учиться!"
Образование должно быть понятным - с этим Вашим тезисом сложно не согласиться! Но каким сочетанием и формой содружества "творчества" и "стандарта" - это огромный вопрос. Особенно если учесть, что достижение нашего предыдущее образование основывалось на германской традиции (с акцентом на Систему и Последовательность) и во многом именно под лозунгами стремления к творчеству ее сейчас разрушают
С уважением, Александр
Re: Пятое правило арифметики
В статье прослеживается рефрен (он несколько раз повторен): все беды - от ЕГЭ. А так ли это? Интересно, а видел ли автор хотя бы раз этот самый ЕГЭ по математике или физике? Сколько там тестов с фиксированными ответами, а сколько - нормальных задач? И как можно "натаскать на ЕГЭ" по той же физике, не научив таки решать задачи?
Как мне представляется, причины катастрофического падения качества школьного образования совсем не в том, в какой форме выпускники сдают экзамены. А, например, в том, что должностной оклад профессора в университете может быть меньше, чем зарплата рабочего у станка, или секретаря в офисе, или даже уборщицы в частной фирме. Не говорю уже о зарплате школьного учителя за пределами МКАДа и КАДа. А еще - в том, что зарплата выпускника, работающего по специальности, не выше, а часто и ниже, чем у его сокурсника, эту специальность пославшего куда подальше.
Можно сколько угодно "поднимать уровень образования", но до тех пор, пока его результаты реально не будут востребованы, общая деградация будет продолжаться. И можно только поклониться тем, кто, несмотря ни на что, пытается спасти ситуацию. Быть может, все-таки дотерпим?..
Re: Пятое правило арифметики
Александр, а какую Вы предполагаете прямую связь между зарплатой профессора (учителя) и методикой его преподавания?
Вот связь между формой экзамена и подстраиванием под нее методики подготовки прослеживается (прослеживалась многими) вполне однозначно. ЕГЭ повышает "объективность", но как раз за счет формализации (увеличение количества задач, выбор ответов и т.д.)Даже с очень большой зарплатой учителю очень затруднительно готовить, а не натаскивать, если ученики (и их родители!) жаждут именно натаскиваться, чтобы получить высокое ЕГЭ. Задумываться в ЕГЭ часто даже вредно - время теряется и много всяких доводов в пользу разных вариантов возникает. "Алгоритмичность" эффективнее при жестких временных рамок и большого количества. Вот только реального понимания (фундаментальности) она обеспечить не может
С уважением, Александр
Re: Пятое правило арифметики
Такую, что если толковый преподаватель может заработать больше, работая, скажем, водителем или кассиром, то много ли толковых преподавателей будут преподавать?
Александр, а Вы видели варианты ЕГЭ по физике и математике? Речь в статье идет именно об этих предметах. Вы уверены, что задания ЕГЭ по этим предметам можно решить без знания самих предметов?
Не знаю, кто как, а лично я в излишней "фундаментальности" нашего образования вижу больше минусов, чем плюсов. Выпускник, который имеет представление о том, что такое синус с косинусом, но ошибающийся при расчете ставки банковского процента в ДВАДЦАТЬ РАЗ (реальный пример!), - по-моему, не самый лучший пример для подражания. Больше скажу: я как-то ради эксперимента попросил нескольких взрослых людей с высшим образованием сделать эту же операцию - ответа, совпадающего с правильным хотя бы с точностью в 50%, не дал НИ ОДИН!
Далее. В нашей фирме (мы делаем всевозможный компьютерный софт) нет проблем найти творческого человека, но большая проблема - найти хорошего исполнителя, умеющего выполнять работу по инструкции, а не по собственному наитию. Я считаю, что это в значительной мере тоже издержки пренебрежения к "алгоритмизированному" образованию и возвеличивания "творческой личности".
Южные корейцы в школе учатся, кстати, оч-ч-чень "алгоритмизированно", но при этом на школьных олимпиадах наших "творцов" частенько бьют. То же самое - спортсмены: на последней зимней (!!!) Олимпиаде Южная Корея завоевала столько же "золота", сколько и Россия. А олимпийское золото голой муштрой не возьмешь. Не говорю уже о том, что "алгоритмизированные" корейцы за 30 лет прошли путь из средневековья к западноевропейскому уровню жизни, а "творческие" россияне за тот же срок прошли путь аккурат в противоположном направлении.
В общем, не вижу я особых преимуществ в том, чтобы в МАССОВОМ образовании напирать на творчество и фундаментальность. Мне в этом отношении куда более по душе американский подход: кто хочет - тот учится (и у него есть для этого все возможности, включая дистанционное обучение у профессоров колледжей и университетов), кто не хочет - того обучают дисциплинированно действовать строго по инструкции.
Разумеется, я не претендую на абсолютную истину - только лишь хочу подчеркнуть "оборотную сторону медали", именуемой "творческим развитием".
С уважением,
Александр.
Re: Пятое правило арифметики
Александр Ильич, Вы так "обличительно" спрашиваете А.Ромащука, а перед этим и автора статьи, что уже хочется спросить и Вас - а Вы сами-то видели? :)
Я уверен, что ЕГЭ по этим предметам можно сдать без знания самих предметов. Просто надо знать, в какой позиции на какой пункт ставить крестик. Как на выборах в 96 году с его бессмертной формулой "Да-Да-Нет-Да" (формулу помнят многие, а вот что было в тех пунктах?). Как при сдаче ЕГЭ в Дагестане, Карачаево-Черкессии и Ямало Ненецком округе, где в прошлом году отличников по физике было поболее, чем в Москве. То есть это действительно работает.
Да Вы сами попробуйте:
Итак, ЕГЭ по физике. 240 минут, 35 заданий.
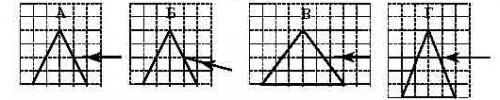
Вот одно из них: Пучок белого света, пройдя через призму, разлагается в спектр. Была выдвинута гипотеза, что ширина спектра, получаемого на стоящем за призмой экране, зависит от угла падения пучка на грань призмы. Необходимо экспериментально проверить эту гипотезу. Какие два опыта из тех, схемы которых представлены ниже, нужно провести для такого исследования?
1) Б и Г
2) Б и В
3) А и Б
4) В и Г
Ради бога, не ошибитесь за те 6 минут, что есть на раздумья.
Вы сейчас рассказали о том, что выпускники не знают как считать сложные проценты. А банковские они, или приплод дрозофил, это вопрос вторичный. Довод не засчитан. Я правильно понимаю, что в Вашей корейской фирме сплошные творцы и проблема найти исполнителей? Вас, кстати, брали как творца или как исполнителя? Про Олимпиаду - это действително крутой довод. Осталось про перекрытие какого-нибудь Енисея. :) Если про школьные олимпиады: Вы могли бы приоткрыть завесу тайны - за счет чего человек, которого учили все время работать только по установленным правилам, побеждает на творческой олимпиаде? Или может быть "алгоритмизированность" была не той, которая натасканность?Да и как дисциплинированный человек может за 30 лет выучить ранее написанные не им учебники, я вполне понимаю. Вот как он, не научившись творить, станет писать новые учебники - это для меня вопрос. О, несомненно. У нас, всего навсего, предлагают убрать первую часть Вашей формулы. Попробуйте вжиться в этот новый образ. Да и я не против правил, просто хотел показать обратную сторону увлечения только ими.
Re: Пятое правило арифметики
Александр, я не ратовал за безмерное увеличение творческости - как раз в первом посте намекал на возникающие сложности, если творчество за счет фундаментальности.
В Ваших примерах мне не хватает оценки понимания. Ученик может вполне алгоритмично считать как косинусы, так и сложные проценты. А может это делать с пониманием (это в смысле гештальтпсихологии). Фундаментальность по-идее должна это обеспечивать, поскольку дает основу и систему. Естественно, часто "фундаментальность" приводила к противоположному результату - многочисленным оторванным знаниям. Обсуждаю это на данном сайте еще и потому, что, как мне кажется, это важно и для ТРИЗ с его акцентом на практичность
По ЕГЭ дальше спорить не готов, поскольку не очень глубоко знаю этот предмет (хотя задания видел)
С уважением, Александр
Re: Пятое правило арифметики
Учительская байка, которую рассказал мне мой отец. Пишу от первого лица.
Как то мне пришлось заменять заболевшего учителя истории в течение месяца в одной из школ Гомеля. Этого учителя все очень хвалили и говорили, что он действительно учит своих учеников (старшие калассы) думать. Мне было очень интересно...
Вызвав ученика (отличника) к доске для опроса я ожидал для начала услышать рассказ об определённом историческом событии, и, затем, его анализ. Вместо этого я услышал, какой из этого события следует сделать ВЫВОД. За вывод я похвалил, но всё таки попросил рассказать о самом событии и его проанализировать. Ученик не смог ни описать ситуацию ни её проанализировать. Он вообще не понимал, что я от него хочу...
По пройденому материалу та же картина.
Материала ученики не знали, но все умели "делать выводы". Более того уже потом выяснилось, что перед каждым уроком по классу ходил "список выводов" которым хорошо успевающие ученики делились с отстающими.
Но на проверяющих из различных ...ОНО всё это действительно производило впечатление...
Re: Пятое правило арифметики
Тест по литературе - no comment...
Имеется нечеткость в формулировке вопроса - есть такой грех в задании. Надо было спросить не об "исследовании" (я, будь исследователем, провел бы все эти опыты), а о "доказательстве", - тогда ответ "А и Б" становится единственно правильным.
Так-то оно так, да не совсем... Сложные проценты умела считать добрая половина опрошенных. А вот ставку банковского процента - нет.
Простой вопрос: магазин предлагает кредит "Десятка". Первый взнос - 10%, затем ежемесячно еще по 10% в течение 10 месяцев. Как Вы думаете, какова процентная ставка по этому вкладу? Варианты: 10%; от 11 до 15%; от 15 до 20%; от 20 до 25%; от 25 до 30%. Ваш ответ? Или проще: в качестве альтернативы предлагается обычный банковский кредит под 22% годовых, тоже с ежемесячным погашением равными долями, - он выгоднее "десятки" или нет?
После того как Вы найдете (верю) правильные ответы, скажите честно: нужно учить эту тему в школе, или лучше поизучать дрозофил?
Неправильно. Я не работаю в корейской фирме. Мо фирма имеет Head office в США, а штат исполнителей - в СПб. Меня нанимали исключительно как исполнителя. Статус "творца" надо было еще заслужить. Но за "творчество" само по себе мне не платят - платят за точное исполнение обязательств перед заказчиками, в том числе в случаях, требующих принятия нестандартных решений (если контракт заключен, но не выполнен, то "его невозможно было выполнить" - для меня не отговорка). Если можно было выполнить проект без творчества - то за "творческие" решения мне могут и зарплату срезать, особенно если заказчик не будет удовлетворен. "Вначале бизнес, потом удовольствие" (с) У. Черчилль...
Тайну успехов корейцев на школьных олимпиадах раскрыть не могу, ибо "со свечкой не стоял". А вот как победить на школьной олимпиаде без излишнего творчества - знаю не понаслышке. Более того, знаю одного такого товарища, который побеждал на Всесоюзных и республиканских (Украина) олимпиадах по нескольким разным предметам: он просто знал, как решать те или иные задачи.
Что касается написания учебников - это вопрос сложный и немало зависящий от того, что называют менталитетом. Надо понимать, как школьник, растущий в конкретной культуре, будет усваивать материал при той или иной форме его подачи. Корейские учебники для русского школьника (естественно ,в переводе) - смерть. Русские учебники для корейского школьника (естественно, тоже в переводе) - в лучшем случае, малоосмысленный набор слов.
Тем не менее, я не видел еще более толкового учебника иностранного языка, чем учебник корейского для иностранцев, изданный в Корее. Не любой учебник, а вполне конкретный. Он меня просто потряс не только своей систематичностью и продуманностью заданий, но и простотой усвоения материала. Жаль, что это был учебник только лишь начального уровня...
Трудно вжиться... Но ведь, вроде бы, сейчас действует система олимпиад, в том числе и через Интернет? Быть может, не настолько все сумрачно? Увы, судить не берусь: если варианты ЕГЭ еще можно посмотреть в Интернете, то увидеть современную российскую школу вживую - увы, не могу. Ничего не могу сказать по существу вопроса.
Разумеется, истина, как всегда, где-то посередине...
Re: Пятое правило арифметики
Хочется спросить: "А какое же решение верно?" Если это варианты А и Б,то эта задача на смекалку и ничего общего с физикой не имеет. Она не требует знания физических законов. Действительно, странные задачки на ЕГЭ и очень интересно увидеть того, кто их сочиняет.
Re: Пятое правило арифметики
Правильный ответ: А и Б.
Задача конечно же физическая, но на смекалку. Здесь нужно "увидеть", что именно нужно искать на рисунках - то что призма должна быть одна и та же, или одинаковые. Все остальное, что может быть важным в данном случае, остается в данном случае за кадром. Так бывает в школе, но обычно на экзамене преподаватель пытался понять, понимает ли экзаменуемый. Здесь в ответах зашифрован один из важных факторов выполнения эксперимента.
Если заранее знать, на что именно обращать внимание, то тест решается быстро. Для человека "стерильного" возникают вопросы идентификации самих рисунков, а на это уходит время. Я взял один из простых, начальных вопросов, там есть и задачи, которые действительно надо решать. И их тоже надо не просто решить, а решить по "правильной" траектории. То есть проявить не просто ум а "правильный" ум, именно тот, которого ждет составитель вопроса. Неправильным ответом считается любой выход за рамки, даже правильный ответ, данный не в той форме, на которую рассчитывал составитель.
Re: Пятое правило арифметики
удалил
Re: Пятое правило арифметики
ЕГЭ, конечно, вещь в себе (пожалуй даже и для себя). Но это парадоксальным образом напомнило мне об учебных задачах по АРИЗ.
Во всяком случае, классическая ТРИЗ тоже подразувает единственно правильный путь к ответу и, соответственно, единственно правильный ответ. А ведь речь подготовке креативщиков!"
Re: Пятое правило арифметики
А у нас и своих ошибок полно, чего же нам старые и не наши в строку ставить?
Re: Пятое правило арифметики
Вставлю еще один странный для данного сайта комментарий.
Кто-нибудь задавался вопросом о том, какие именно знания-умения-навыки в первую очередь необходимы среднестатистическому выпускнику среднестатистической российской школы? Какую именно работу будет выполнять этот персонаж в течение первых, скажем, 10-15 лет после окончания школы? За что ему будут, в конце концов, деньги платить? Многие ли уверены, что именно за креативность? Или все же за то, что он будет уметь делать то, что начальник скажет? Быть может, этот начальник не всегда абсолютный идиот?
Далее - к экзаменам. Выпускники советской школы наверняка помнят отдельных отличников (чаще женского пола, иногда не отличниц, а "хорошисток" с 2-3 четверками в табеле), чьи школьные успехи можно охарактеризовать словом "зубрилка". Традиционные экзамены они всегда сдавали классно! Сильно ли это помогало им в послешкольной жизни? И что конкретно ухудшится от того, что их же "натаскают" и на ЕГЭ? Не все ли им равно, в какой конкретно форме материал зазубривать?
Далее - к тем, кто мог бы реально пострадать от того, что традиционные экзамены по физике и математике (подчеркиваю: в статье речь идет только об этих предметах) заменяются жуткими-жуткими тестами (в которых, вообще-то, бОльшую часть занимают самые обычные задачи, если кто не в курсе). Человек, понимааашь, знает в совершенстве всю теорию, может рассказать любую тему так, что аж заслушаешься, но вот беда - задачки решать почему-то не умеет... Ну, не научили его этому. Быть может, такие персонажи тоже кому-то знакомы? Ну и как, сильно ли ухудшится интеллектуальный уровень студенчества от того, что они таки не пройдут новые кошмарные испытания?
Так все-таки, что именно ухудшается от того, что вместо обычных экзаменов абитуриенты сдают этот ненавистный ЕГЭ? И кто именно от этого может проиграть, не поступив на свое законное бюджетное место? И... так ли велика для общества ТАКАЯ потеря?
Re: Пятое правило арифметики
Оно, конечно, так. Поэтому я и написал "парадоксальным образом". Однако ж рецидивы случаются! И не так уж и редко. А вообще-то, нас тоже натаскивали. Втлорое полугодие 10-го класса не столько учили, сколько именно натаскивали на экзамены.
Так что вопрос не простой. Хотя лично мне ЕГЭ тоже не нравится, но вот обосновать это неубиваемыми аргументами - не могу
Re: Пятое правило арифметики
Думаю, что мы в действительности плох понимаем, что человеку, а точнее человечеству, нужно. Поэтому, похоже, спорим о двух сторонах одной медали - кративность специалиста, его исполнительность. Наверное, человечеству нужно и то и другое. Другое дело - в каких пропорциях. Ответить на это крайне сложно. Вероятее всего, что в зависимости от конкретного времени и места возниает то или иное соотношение.
Одно остается неизменным - для каждого вида деятельности нужен хороший инструмент и понимание, как его выбирать.
С пожеланием всегда иметь под руками остр заточенный инструмент.
А.Гасанов
Re: Пятое правило арифметики
Неужели этим вопросом: "Что человеку, а точнее - человечеству, нужно?" никто не занимался? Или все отвечали настолько по-разному, что общность нельзя выявить?
Давайте, перейдем от слов о плохом понимании, к действиям и проделаем эксперимент - начнем отвечать на вопрос "Что мне нужно?" или "Почему я это делаю?", начиная с самых элементарных действий. Ведь раз мы их производим, значит они нам зачем-то нужны...
Начнем с действия А, а потом начнем углублять понимание по цепочке: Я совершил действие А. Зачем (для чего, с какой целью) я совершил действие А?
Бывает, ответить просто - для того, чтобы достичь цель Б. Или совершить следующее действие Б. Если трудно ответить на вопрос о причине совершения действия А, можно спросить по-другому: "Что произойдет, если я не совершу действие А?"
Это будет как раз в русле того, что "наука - это знание причин". Давайте построим цепочку причин - Для чего? или Почему? - как можно более длинную. Вдруг, появится что-то общее, а?
Успехов,
AlexZ