В предыдущей статье [1] были сформулированы требования к семействам «идеальных» кривых. Целью представленной работы является анализ известных математических моделей, пригодных для описания развития Технических Систем (ТС).
Исходя из высказанных ранее предположений о характере зависимостей параметров систем от времени, предлагаемая для описания модель должна отвечать нескольким критериям.
Модель должна:
- быть «привязана» к точкам, расположенным на начальном участке кривой;
- описывать несимметричные кривые;
- давать возможность спрогнозировать возможное значение технического предела развития.
Посколькузависимости изменения параметров систем от времени достаточно часто описываются S-кривыми, то вопрос их описания уже давно привлекает исследователей. В работе [2] для этого были проанализированы различные модели (линейная, простая экспоненциальная, логистическая). В работе однозначно показано, что наилучшим вариантом описания является логистическая модель.
Рассмотрим сначала модель, известную как логистическая кривая, кривая Перла — Рида, или просто кривая Перла. Ее уравнение имеет вид:
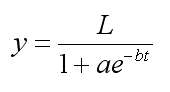 (1)
(1)
В этом уравнении L является верхним пределом переменной у, а а и b — параметры. Кривая имеет начальное значение, равное 0, при t, равном минус бесконечности, и достигает предельного значения L при t, равном плюс бесконечности. (Если начальное значение у0 ≠ 0, то оно может быть прибавлено к правой части уравнения как константа.). Кривая симметрична относительно точки перегиба, верхняя половина является отражением нижней.
Уравнение (1) легко приводится к линейному виду:
![]() (2)
(2)
Коэффициенты такого уравнения могут быть определены методом наименьших квадратов.
Как уже отмечалось, наибольшую активность в попытках найти математическое описание для S-кривых сейчас проявляет Д.Кучерявый. В своей работе [3] он использует уравнение:
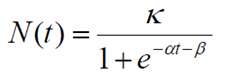 (3)
(3)
где a – параметр роста, k – предел роста, b – параметр времени, за которое параметр достигает значения 0.5k. Легко видеть, что данное уравнение является разновидностью модели Перла (См. Уравнение 1).
В работе [4] приведены некоторые соображения, касающиеся использования «логистической кривой» в практических расчетах. К сожалению, авторы работы не рассмотрели такой важнейший для практики вопрос, как точность исходных данных, в связи с чем ряд рекомендаций, приведенных в этой работе, особенно в части использования производных высоких порядков, следует, на наш взгляд, воспринимать критически.
Другая часто используемая кривая роста названа именем Бенджамина Гомперца, английского статистика и математика, который первым предложил эту кривую как закон поведения уровней смертности. Уравнение кривой Гомперца имеет вид:
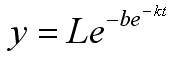 (4)
(4)
Как и кривая Перла, кривая Гомперца простирается от нуля при t, равном минус бесконечности, до верхнего предела L при t, равном плюс бесконечности. Кривая, однако, несимметрична. Кривая Гомперца также легко приводится к линейному виду:
![]() (5)
(5)
Как следует из анализа уравнений (2) и (5), модели Перла и Гомперца слишком «привязаны» именно к конечным точкам зависимости, в то время, как наиболее достоверные данные находятся как раз в начальной области. Это существенно осложняет возможность надежного прогноза.
В работе [5] рассмотрены применения различных видов уравнений для описания количественных кривых зависимости массы добываемой нефти от времени, которые имеют форму, близкую к S-образной. В ней показано, что логистические кривые справедливы только для случая линейного падения скорости роста рассмотренного параметра. Эта модель так называемого «подавляемого роста» соответствует, как уже было отмечено, только симметричным кривым.
В той же работе было замечено, что для описания несимметричных кривых могут быть использованы уравнения, использующие так называемое ядро Кольрауша, которое соответствует растянутой во времени экспоненте и является аналогом распределения Вейбулла в математике. Последняя зависимость имеет вид:
![]() (6)
(6)
где Y0, b, и t1 – параметры модели.
Уравнение Кольрауша [6] отличается от него наличием еще одного эмпирического коэффициента – показателя степени b:
![]() (7)
(7)
где Y0 и y∞ – начальное и конечное (предельное) значения выходной переменной. Это уравнение широко используется для описания релаксационных процессов разной природы неорганических стеклах [7, 8].
Подобное уравнение ранее было использовано для описания изменения механических характеристик натуральных, искусственных и синтетических волокон при их пластификации [9] в виде:
Подобное уравнение ранее было использовано для описания изменения механических характеристик натуральных, искусственных и синтетических волокон при их пластификации [8] в виде:
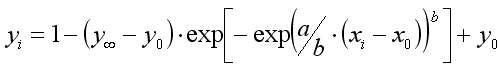 (8)
(8)
где y0, x0 – координаты начальной точки зависимости, y∞ – предельное значение параметра, a, b – параметры модели. Такое уравнение легко преобразуется в линейный вид:
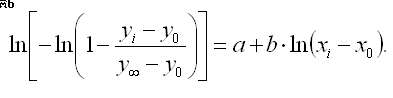 (9)
(9)
Обычно в технологическом прогнозировании верхний предел L определен известными физическими ограничениями для конкретного технологического решения. Следует помнить, однако, что на практике, помимо физических ограничений, могут иметь место и другие, в том числе и искусственно созданные (например, законодательные ограничения уровня шума у самолетов). Вопрос об остановках в развитии систем был рассмотрен нами в [10].
Пример сравнительного описания модельной кривой с помощью предлагаемой экспоненциальной модели (8) и логистических моделей Перла (3) и Гомперца (4), при одинаковых значениях пределов представлен на Рис.1.. Использованы модельные кривые из работы [1, Рис. 2]. Среднеквадратические ошибки расчета представлена в Таблице.
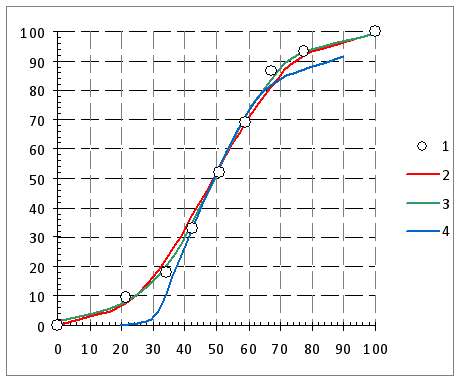
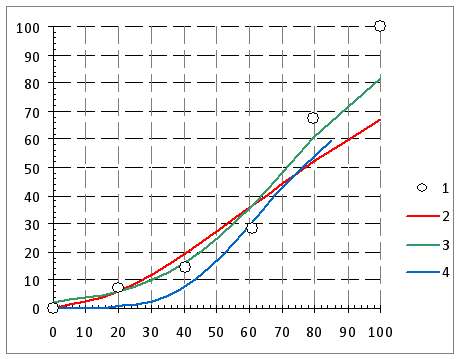
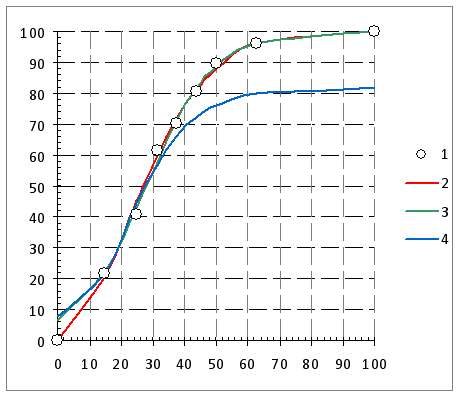
Рис.1. Описание модельных кривых 1, 3 и 5 соответственно на Рис. 2 из работы [1] в относительных координатах (1) по предлагаемой экспоненциальной модели (2) и по уравнениям Перла (3) и Гомперца (4). Для сравнения были выбраны крайние случаи и средний вариант.
Табл. Среднеквадратические ошибка расчета по модельным уравнениям.

Из приведенной таблицы видно, что уравнение Гомперца уступает по описательной возможности уравнениям Перла и Кольрауша для всех рассмотренных случаев. Что касается сравнения уравнений Перла и Кольрауша, то для рассмотренных случаев преимущество какого-либо из них не кажется очевидным. Однако легко видеть, что уравнение Перла во всех случаях имеет различные отклонения при описании разных участков экспериментальной кривой. Как уже отмечалось ранее, эти отклонения максимальны на начальном участке кривых, то есть в наиболее достоверной области данных. Поэтому, мы полагаем, что предпочтение должно быть отдано именно уравнению на основе Кольрауша.
Проверим теперь способность применения экспоненциальной модели (8) для описания реальных зависимостей. На Рис. 2 представлен пример описания этим уравнением временной зависимости эффективности источников света.
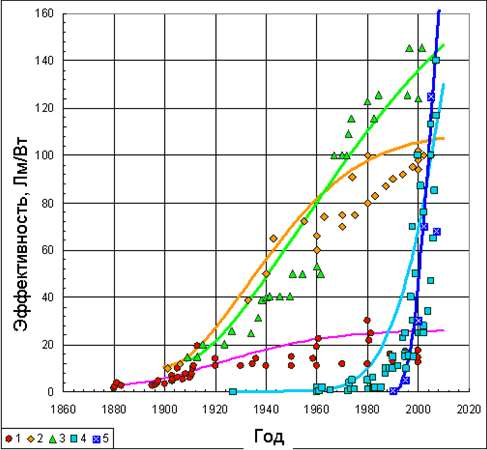
Рис. 2. Зависимость эффективности от времени для: ламп накаливания (1), флуоресцентных ламп (2), дуговых ламп (3), светодиодов (4) и органических светодиодов (5). Точки – экспериментальные данные, линии – расчет по уравнению (8).
Расчет зависимость эффективности от времени источников света по уравнению (2) показал, что среднеквадратическая ошибка расчетов не превышала 20%, что для фактических данных с учетом их разброса вполне удовлетворительно. То есть, предлагаемая модель на основе уравнения Кольрауша описывает реальные зависимости более корректно, чем логистические кривые.
Однако, одним из преимуществ данной модели является то, что в логарифмических координатах она с достаточной точностью описывается прямыми линиями (См. Рис.3).
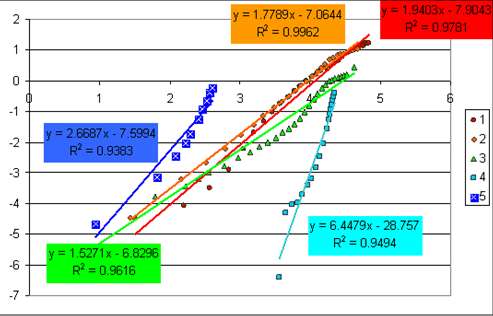
Рис.3. Зависимость эффективности от времени в логарифмических координатах для: ламп накаливания (1), флуоресцентных ламп (2), дуговых ламп (3), светодиодов (4) и органических светодиодов (5). Точки – экспериментальные данные, линии – расчет по уравнению (8).
К сожалению, для случаев, у которых не определены пределы роста и известны только начальные точки зависимости, применение уравнения (8) является достаточно проблематичным.
Теоретически эту проблему можно решить, используя линейность этого уравнения в логарифмических координатах. То есть, возможно, задавшись примерным значением предельного значения параметра y∞, проводить подбор уточненного значения этого параметра, исходя из требований линейности этой зависимости.
Если принять это предположение, то появляется возможность подобрать соответствующие параметры уравнения, используя методы наименьших квадратов, или градиентного спуска. Однако следует учитывать, что неопределенность верхнего предела может значительно снизить надежность таких расчетов, имея в виду и тот факт, что физические пределы развития достигаются реальными ТС весьма редко.
Кроме модели Кольрауша S-образные кривые могут быть также описаны с помощью и других моделей, например таких, как модель роста Капицы-Баренблатта, которая соответствует гиперболическому росту параметра, который в определенный момент сменяется «катастрофой», то есть сменой механизма роста. Однако эта модель, как и все предшествующие, основана на предположении о том, что кривая роста может быть вычислена исходя только лишь из характеристик самой системы, без учета надсистемных факторов. На наш взгляд, это существенно ограничивает область применимости таких моделей. В частности, пока представляется проблематичным описывать с их помощью кривые, на которых имеются задержки и остановки, сменяющиеся в определенный момент продолжением роста (см. примеры таких кривых в [9]).
Заключение
Сопоставление известных простых моделей роста показателей развивающихся систем показало, что наиболее предпочтительной из них является модель Кольрауша («дробная экспонента»). Она позволяет учитывать, в частности, асимметрию реально наблюдаемых кривых. Однако применимость всех рассмотренных моделей ограничена «стандартным» ходом развития, не предусматривающим задержек и остановок в ходе движения по S-образной кривой. В следующей публикации мы рассмотрим более сложные модели на основе дифференциальных уравнений, которые, по крайней мере принципиально, позволяют описать и такие ситуации тоже.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
- Кынин А. Модель развития технических систем, http://www.metodolog.ru/node/740
- Stephen R. Lawrence S-Curve Forecasting Stephen R. Lawrence
- Dmitry KUCHARAVY, Roland DE GUIO / Application of S-shaped curve / ETRIA TRIZ FUTURE CONFERENCE 2007, Frankfurt, November 7 / 2007
- Бердоносов В., Памазанов Р. О выражении для логистической кривой, http://www.metodolog.ru/node/249
- Соколов В.А. Эволюционные уравнения, как феноменологические модели разработки нефтегазовых залежей. Нефтегазовое дело, 2006
- Kohlrausch F. Über die elastische Nachwirkung bei der Torsion // Pogg. Ann., 1863, Bd 119, S.337-368
- Scherer G.W. Relaxation in glass and composites // New York: Wiley, 1986, 348 p.
- Мазурин О. В. Стеклование. Ленинград: Наука, 1986, 158 с.
- Гребенников С.Ф., Кынин А.Т., Клюев Л.Е. Сорбция водяного пара текстильными материалами. // Вестник Санкт-Петербургского государственного университета технологии и дизайна. - 1998, №2, С.176-183.
- Кынин А., Привень А. Задержки и остановки в развитии технических систем, http://www.metodolog.ru/node/910
Комментарии
Re: Простейшие модели развития ...
inohod
какая публикация нечитабельная - имею в виду графику
Re: Простейшие модели развития ...
Я отправил сегодня Редактору все необходимые файлы - недеюсь, в самое ближайшее время дефекты будут устранены.
К сожалению, до появления публикации на сайте нет у авторов возможности понять, как то или иное изображение будет выглядеть в браузере. Надеюсь, приноровимся со временем.
С уважением,
Александр.
Re: Простейшие модели развития ...
А также - действительно ли имеет место зависимость, и для какой именно характеристики можно так говорить корректно?
Ведь линия, соединяющая две соседние точки, - это авторская интерпретация реальных событий. А так это было или не так - при учете того момента, что "зависимость" условная, историческая, так сказать - большой вопрос.
И если авторы считают корректным соединять точки так, как они это делают, то корректным выглядит и последующее выведение формулы, которая такой предположительной графической зависимости придала бы статус достоверности, действительности...
Потому что, если такой формулы нет, или же ее аналог не дает ясного понимания любому желающему, что именно он спрогнозирует подстановкой в формулу интересующих его параметров, то не составляет труда понять, что авторы в очередной раз не вышли за пределы первичной аналогии.
Осознание

==ИИ-->
Re: Простейшие модели развития ...
Господа, чего вы привязались к этим S-образинам?
Что мало других, не уступающих по неточности отражения реальности, инструментов ТРИЗ?
Много.
И даже математические модели для них не построены.
Вот хотя бы таблица противоречий - какая классная математическая модель выбора оптимальной пары параметров ногла бы получиться!
Куда там какой-то "занюханной" логистической кривой!
А если к этому добавить математическую модель оптимального сочетания пар оптимальных параметров и присовокупить к этому уравнение выделения из всего списка, предложенных оптимальными сочетаниями оптимальных пар, приёмов нескольких, работающих наилучшим образам, со статистически минимальной погрешностью +/- 25% - консервативные исследователи S-образин просто захлебнутся собственной слюной.
Да...
Совсем забыл...
И назвать надо соответствующим образом...
Типа... "К вопросу об элементарных моделях использования таблицы технических противоречих"
Re: Простейшие модели развития ...
Уважаемый Григорий,
Не затруднит ли Вас пояснить, какое именно отношение имеет Ваше предложение к количественному предсказанию роста значений параметров технических систем? Быть может, я чего-то очень важного не понял, - но, по-моему, Вы говорите о чем-то малость другом, что находится за пределами тематики данной статьи...
Заранее благодарен,
Александр.
Re: Простейшие модели развития ...
Не затруднит.
И то и другое, по-моему, что-то вроде попытки построения математической модели гадания на кофейной гуще путём анализа "основных" параметров, как то
размер, форма, материал чашки, температура гущи (после того, как выпили кофе), степень помола, степень густоты и т.д.
Но можете продолжать.
Я высказал своё мнение один раз и больше влезать в "научное" обсуждение не буду.
Re: Простейшие модели развития ...
Уважаемый Григорий, Ваше право идти своим путем, а наше - своим. Мы с АКыном в этом смысле ба-альшие консерваторы и идем потихоньку - без революций и потрясания основ, а, напротив, пытаясь понять то, что уже сделано нашими предшественниками, и на этой самой, имеющейся уже основе выстроить нечто новое.
"Эсобразину" ведь только ленивый не пинал и в помойное ведро не выбрасывал. А мы вот думаем, что с пинками здесь несколько поторопились, и что без математического (количественного, а не качественного!) описания этой самой "никому не нужной", "сугубо теоретиццской" кривульки нормальную модель развития ТС построить все равно не получится. Что поделать - разница в подходах. Для науки это нормально. А чей подход ближе к истине - жизнь покажет. Скорее всего, как это обычно случается, каждый из нас в чем-то прав, а в чем-то не очень.
Успехов!
С уважением,
Александр.
Re: Простейшие модели развития ...
Разумеется, Вы совершенно правы, Геннадий Иванович: зависимость условная, и интерпретация авторская, да и сам процесс в общем-то не сильно ясен...
...Ровно такая же ситуация - и даже хуже! - наблюдается при... расчете свойств стекол по их химическому составу. Ну, сварили ряд стекол разных составов, померили их свойства, соединили кривульками... Процесс-то где? Что там точками-то соединено - что в промежутках между этими сваренными стеклышками? Пустота ведь, нет там ничего, никаких объектов нету, ноль. И "зависимость" из пальца высосанная - какая ж это зависимость, если данные для РАЗНЫХ объектов, изготовленных к тому же в РАЗНОЕ время (с интервалом эдак лет в сто) и вдобавок из РАЗНЫХ исходных компонентов, соединили ОДНОЙ кривулькой? Да еще часть точек с нее удалили, чтоб другим неповадно было. Страх, жуть и полный кошмар - в общем, это не ужас, а ужас-ужас-ужас!
...Если б так оно и было, то никогда б Вы не сидели за своим монитором. Ибо стеклышко там оченно специальное, и состав этого чудо-стеклышка без этих кривулек не подобрать было никак... А ведь и подобрали, и сварили, и в папирус вытянули (примерно 0.4 мм у этого стеклышка толщина), хотя и зависимость там условная, и интерпретация авторская, и процесса за кривулиной не видно...
Быть может, все дело в том, чтобы... не бояться поставить вопрос, который "нельзя" ставить из "принципиальных" соображений, а просто его... решать?
С уважением,
Александр.
Re: Простейшие модели развития ...
Процесс - чего?
Ваш пример с расчетом и варкой стекол - без увязки со смыслом статьи - как-то еще больше запутал
Следует ли из цитаты, что кривые для расчета химического состава стекол Вы также представляете S-образной кривой? Или они и до этого имели такую форму?
Решать или не решать - это прерогатива авторов статьи. А читателям хочется понять, можно ли брать их подход и сразу же использовать, или же сначала надо некие приемы выкопать из ее содержания ...
Осознание

==ИИ-->
Re: Простейшие модели развития ...
Я тоже "тряски" не люблю.
И ремарки мои касаются не мелкотемья, а бесполезности.
А по поводу того, что у каждого есть право идти своим путём (и совершать свои ошибки) - Вы правы.
Re: Простейшие модели развития ...
Геннадий Иванович, прошу прощения, если чем Вас запутал. Не хотел. Честно.
Про процесс. Я имел в виду Ваше заявление про то, что "зависимость условная, а интерпретация авторская". Так обычно говорят как раз про зависимости, не отражающие конкретный процесс: мол, надергали фактов и строят кривульки, соединяя точки как на душу взбредет. Я и привел пример, когда факты вроде бы тоже надерганы не пойми откуда, а зависимость, тем не менее, есть, и ее знание полезно. Если Вы имели в виду что-то другое, говоря об "условной зависиммости" и "авторской интерпретации" - то что именно? Проведение линии через множество точек - вроде бы совершенно стандартная для науки процедура, разве нет?
Форма этих зависимостей свойств стекол от их состава (а я имел в виду именно эти зависимости) бывает разной, в том числе и эс-образной - простите за невольный каламбур.
Это уже на усмотрение читателя. Данная статья не содержит "подхода авторов статьи", а содержит только лишь обзор некоторых подходов других авторов и некоторые выводы касаемо того, какой из этих подходов авторам статьи кажется лучше других подходов, представленных в статье.
"Подход авторов статьи" же заключается в том, чтобы на основе известных решений и с учетом их достоинств и недостатков выработать собственный подход. Без революций, без суеты и с максимальным учетом и использованием уже сделанного до нас, в том числе и в части описания "эсобразины" как наиболее типичного вида кривой изменения параметров ТС со временем, прежде всего для систем с одинкаовым предназначением и фиксированным принципом действия.
С уважением,
Александр.
Re: Простейшие модели развития ...
В данном случае меня не сами интерполяция или аппроксимация как таковые интересуют, а о чем говорят их результаты.
Например, искусственная траектория кривой может лежать как ниже реальной точки, так и выше ее. О чем говорит этот момент?
И чем является эта (условно перенесенная) точка кривой, какой ее смысл с позиции ТРИЗ? Это локальная идеальность для реально достигнутого параметра в данной временной координате?
Или что-то иное?
Понятно теперь, что это нечто вроде состояния вопроса.
Принцип действия обычно с системой вроде как не соотносится, ибо он всегда предопределяет наличие нескольких основных функций, а не одной. Поэтому - что в данном статье понимается под системой, в т.ч. - технической?
Осознание

==ИИ-->
Re: Простейшие модели развития ...
Геннадий Иванович, хорошие вопросы задаете! Спасибо. Не все из них, правда, кажутся мне хорошими, но это, может быть, уже моя проблема, а не Ваша.
Сам по себе этот факт мне, по правде сказать, не говорит ровно ни о чем. Технические системы не солдаты, чтобы идти строем и поддерживать высоту поднимания каждой ноги. Разброс, естественно, есть и будет всегда и по всем количественным характеристикам.
Я бы не торопился говорить здесь уже про идеальность. Идеальность - это не одна характеристика, а соотношение, по крайней мере, трех: двух параметров, находящихся в противоречии (иначе бы была не "идеальность", а "максимальность"), и суммы факторов расплат. Здесь же - только одна характеристика, которая может лишь коррелировать с идеальностью, но не определять ее полностью.
Честно говоря, этого не понял. Может ли быть техническая система БЕЗ принципа действия?!
А что касается непременного наличия нескольких основных функций - то какие это функции, например, у стиральной машины?..
Наш обстоятельный ответ на этот вопрос будет дан в одной из следующих статей, которая сейчас готовится к печати. Просто нельзя же весь "Методолог" забить целиком нашими статьями! Их и так публикуется много, согласитесь: куда ж еще больше-то? Поэтому, пожалуйста, потерпите немного - там, на той ветке, и подискутируем, если будет угодно. А в этой статье приведены характеристики весьма конкретных штуковин - и каждую из них мы считаем технической системой.
С уважением,
Александр.
Re: Простейшие модели развития ...
Понятно. Значит, этот момент какой-либо пользы не приносит.
Понятно. Значит, и этот момент S-образной кривой какой-либо пользы не приносит.
А с чем соотнесен принцип действия в ТС ? С надсистемой? С ней самой? С подсистемами? Другими словами, к чему в системной среде относится действие принципа, точнее - его под-действия?
Основных функций - всегда несколько, в отличие от главной. Ибо все они диктуются надсистемой, а также смыслом того, что Вы понимаете под системой и технической системой. Лично мне этот момент видится важным, т.к. в ТРИЗ исторически сложилось двойственное толкование смысла ТС. Что, с одной стороны, вообще-то неправильно, а с другой - затрудняет понимание смысла направления развития ТС (в сторону идеальности).
Эта Ваша безусловная прерогатива, конечно.
Но она конфликтует с Вашим же пониманием идеальности ТС, как мне представляется. Ибо если графики этой статьи не могут быть корректно соотнесены со смыслом идеальности, то о каком тогда развитии ТС говорит название этой статьи?
Надеюсь также, что следующая статья будет более информативной в этом плане, раз Вы обещаете это :)
Осознание

==ИИ-->
Re: Простейшие модели развития ...
Привет всем!
Извините за задержку, но я сейчас на каникулах в Питере.
Извиняюсь также за излишнюю дидактичность, но каков вопрос – таков и ответ...
Поэтому, чтобы не скатываться на уровень спора Остапа с ксензами рассмотрим все не в режиме дзоба-дзоба (быстро-быстро, кит.), а ибу-ибу (шаг за шагом, кит.).
1. И так, что такое Эс-кривые? По ТРИЗ это зависимость между идеальностью системы и временем жизни. Правда, поскольку идеальность понятие абстрактное, то это временная зависимость от времени какого либо одиночного, либо комплексного параметра. Кстати, именно так эти кривые и рассматриваются международным научным сообществом, которое о ТРИЗ, как правило, и не слыхало.
Первым шагом было создание предмета для обсуждения, что и было сделано в статьях:
Кынин А.Т. РАЗВИТИЕ ИСТОЧНИКОВ СВЕТА http://www.metodolog.ru/01228/01228.html
Кынин А.Т. / 2. РЕСУРСЫ РАЗВИТИЯ ТЕХНИЧЕСКИХ СИСТЕМ 2009.10.15http://www.metodolog.ru/node/341
Кынин А.Т. / 3. РОСТ И РАЗВИТИЕ ТРАНСПОРТНЫХ СИСТЕМ: 3.1. Транспорт 2009.10.15http://www.metodolog.ru/node/359
Кынин А.Т. /3. РОСТ И РАЗВИТИЕ ТРАНСПОРТНЫХ СИСТЕМ: 3.2. Водный транспорт 28.01.2010http://www.metodolog.ru/node/445
Кынин А.Т. Леняшин В.А., Фейгенсон Н.Б. /3. РОСТ И РАЗВИТИЕ ТРАНСПОРТНЫХ СИСТЕМ. 3.3 Наземный транспорт 04.02.2010 http://www.metodolog.ru/node/452
Кынин А.Т. / 3. РОСТ И РАЗВИТИЕ ТРАНСПОРТНЫХ СИСТЕМ: 3.4 Воздушный авиационный транспорт / 2010.02.12 http://www.metodolog.ru/node/456
Кынин А.Т. / 4. РАЗВИТИЕ ТЕХНИЧЕСКИХ СИСТЕМ ОТОБРАЖЕНИЯ ИНФОРМАЦИИ 4.2 Принтеры и печать /http://www.metodolog.ru/node/462
Кынин А.Т. / 5. РАЗВИТИЕ СИСТЕМ ВООРУЖЕНИЯ 5.1 Сухопутная ствольная артиллерия и ракетное оружие /http://www.metodolog.ru/node/487 , http://www.metodolog.ru/node/495
В этих статьях с минимальными домыслами автора была представлена часть коллекции по развитию ТС. И представьте себе, огибающая кривая для большей части зависимостей действительно имеет Эс-образную форму.
2. Поэтому следующим шагом была систематизация таких данных:
Кынин А. , В. Леняшин, Н.Фейгенсон. / ВЫБОР ПАРАМЕТРОВ ДЛЯ ОПИСАНИЯ РАЗВИТИЯ ТЕХНИЧЕСКИХ СИСТЕМ ВДОЛЬ «ЛИНИИ ЖИЗНИ» http://www.metodolog.ru/01697/01697.html
Там было показано, что такая форма характерна в первую очередь для систем либо с одним главным параметром (например, рекордных), либо с комплексным параметром.
Однако для многих систем была отмечена размытость области параметров.
3. Поэтому были рассмотрены случаи их сегментации: «Кынин А.Т. / СЕГМЕНТАЦИЯ S-КРИВЫХ» 2010.01.14 http://www.metodolog.ru/node/428, где было показано, что случайного «облака» параметров не существует, а значения ложатся на группы линий, соответствующих различным требованиям к системам. Например, дальности полета самолетов соответствуют требованиям малой, средней, большой дальности и т.д.
4. Рассмотрение индивидуальных Эс-кривых также показало, что в процессе развития случаются остановки и задержки, что было проанализировано в: «Задержки и остановки в развитии технических систем» http://www.metodolog.ru/node/910
5. Для различных ТС, выполняющих одинаковые функции, но использующих разные принципы действия (семейства, например железнодорожный транспорт) характерны различные формы эс-кривых. Требования к таким кривым были сформулированы в: «Модель развития технических систем» http://www.metodolog.ru/node/740
6. На базе сформулированных требований были предложены «Простейшие модели развития технических систем» http://www.metodolog.ru/node/940, где было показано, что наиболее адекватно такие кривые могут быть описаны уравнениями типа Кольрауша.
Теперь немного о моделях и прогнозах. Зачем вообще эти «яйцеголовые» веками пытаются любую ерунду описать уравнением и, когда это удается, прыгают от радости и удостаиваются увековечить свое имя на найденной формуле?
Дело в том, что только формула (т.е. модель) какого-либо явления позволяет не только описать его, но и прогнозировать изменение в областях, которые по тем, или иным причинам недоступны. Например, предсказать будущие изменения. В нашем случае даже не изменения, а возможные требования потребителей к параметрам систем. Пример – закон Мура (хотя это не закон, и не Мура...).
Моделирование – это отдельная область науки, которая не исчерпывается мудрыми предложениями «натянуть кривую на синус». К сожалению, это не проходят в тех учреждениях, где, видимо, обучались уважаемые коллеги, дающие такие мудрые советы. Между прочим, есть научные журналы в Европе, которые только этим и занимаются, например: http://www.elsevier.com/wps/find/journaldescription.cws_home/505740/desc...
Открою Вам большой секрет. ЛЮБУЮ кривую можно прекрасно описать полиномом, Только толку с такого описания не будет никакого. И только модель, коэффициенты которой несут смысловую нагрузку, может быть использована для прогнозов.
Но это уже другая история, так что ждите, ПРОДОЛЖЕНИЕ СЛЕДУЕТ.
С уважением, Ваш АКын
Re: Простейшие модели развития ...
Обсуждение данной темы закрыто.